Catégories: Articles en vedette » Électriciens débutants
Nombre de fois vus: 4409
Commentaires sur l'article: 0
Comment calculer la température du filament d'une lampe à incandescence en mode nominal
Comme vous le savez, avec l'augmentation de la température du métal, sa résistance électrique augmente. Pour divers métaux, en lien avec ce phénomène, son propre coefficient de résistance en température α est caractéristique, ce qui peut être facilement trouvé dans le livre de référence.
La raison de ce phénomène est que les vibrations thermiques des ions du réseau cristallin métallique deviennent plus intenses avec l'augmentation de la température, et les électrons de conduction qui forment le courant entrent en collision avec eux plus souvent, dépensant plus d'énergie pour ces collisions. Et puisque le courant lui-même (selon la loi Joule-Lenz) conduit à l'échauffement du conducteur, dès que le courant commence à traverser le conducteur, la résistance de ce conducteur commence immédiatement à augmenter.
De même, la résistance du filament de la lampe augmente lorsqu'elle est connectée à une source d'alimentation. Trouvons la température du filament de la lampe dans le mode nominal de son fonctionnement.

Le coefficient de température de résistance du tungstène (à partir duquel est fabriqué le filament d'une lampe à incandescence) est α = 0,0045 / K, et il est associé à un changement de résistance (avec un changement de température) par la relation suivante:
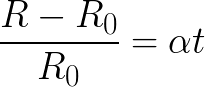
Ici:
Résistance R0 du filament à 0 ° C;
R-résistance du filament à la température actuelle t.
La résistance R0 du filament incandescent à 0 ° C ne nous est pas connue, elle doit maintenant être déterminée indirectement. Pour ce faire, nous mesurons d'abord avec un multimètre la résistance de la lampe à température ambiante.
Ensuite, jetez un œil au thermomètre de la pièce et découvrez ainsi la température de l'air dans la pièce.
Si nous supposons que le filament froid de la lampe a exactement la même température que l'air dans la pièce, la résistance de la lampe à 0 ° C est facilement déterminée par la formule:
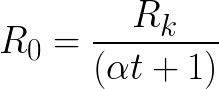
Il faut remplacer ici:
t-température dans la pièce (par thermomètre);
Rk-résistance du filament de la lampe à la température actuelle dans la pièce (mesurable avec un multimètre).
Donc, maintenant nous connaissons la résistance R0 du filament de notre lampe à 0 ° C. Maintenant, connaissant la puissance nominale de la lampe et sa tension nominale, nous déterminons purement mathématiquement sa résistance nominale Rn selon la formule bien connue suivante:
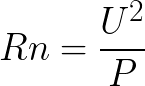
Nous substituons ici les données indiquées directement sur la lampe:
Tension U de la lampe;
Puissance nominale de la lampe P.
Maintenant, nous apportons la toute première formule sous la forme suivante, et substituons la résistance nominale Rn qui vient d'être trouvée, et la résistance R0 à 0 ° С, qui a été trouvée ci-dessus, ainsi que le coefficient de température de résistance α = 0,0045 / K pour le tungstène (tiré du livre de référence):
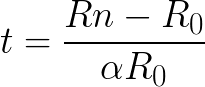
Nous avons donc trouvé la température réelle du filament de la lampe en état de fonctionnement, ne la mesurant pas directement, mais connaissant uniquement la puissance nominale P, la tension nominale du réseau U, la résistance au froid Rk, la température ambiante t et le coefficient de température de la résistance au tungstène α.
Voir aussi sur electro-fr.tomathouse.com
:
