Ce qui détermine le courant de câble admissible à long terme

Qu'est-ce qui détermine le courant de câble admissible à long terme? Pour répondre à cette question, nous devrons considérer les processus thermiques transitoires qui se produisent dans des conditions où un courant électrique traverse le conducteur. Chauffer et refroidir un conducteur, sa température, sa connexion avec la résistance et la section - tout cela fera l'objet de cet article.

Processus de transition

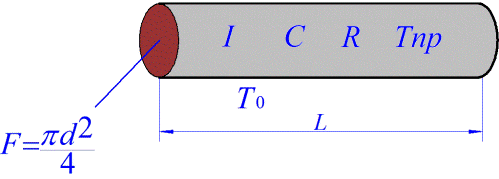
Considérons tout d'abord un conducteur cylindrique conventionnel de longueur L, diamètre d, section transversale F, résistance R, volume V, évidemment égal à F * L, à travers lequel passe le courant I, la chaleur spécifique du métal dont le conducteur est fait - C, la masse du conducteur est égal à

m = V * Ω,

où Ω est la densité du métal du conducteur, S = pi * d * L est la zone de la paroi latérale à travers laquelle le refroidissement se produit, Tpr est la température actuelle du conducteur, T0 est la température ambiante et, par conséquent, T = Tpr - T0 est le changement de température. KTP est le coefficient de transfert de chaleur, caractérisant numériquement la quantité de chaleur transférée d'une surface unitaire d'un conducteur en 1 seconde à une différence de température de 1 degré.

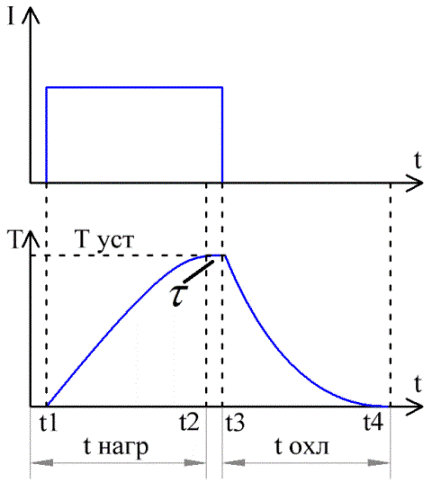
La figure montre les graphiques du courant et de la température dans le conducteur au fil du temps. Du temps t1 au temps t3, le courant I a traversé le conducteur.

Ici, vous pouvez voir comment, après avoir mis le courant, la température du conducteur augmente progressivement et, au temps t2, elle cesse d'augmenter, se stabilise. Mais après coupure du courant à l'instant t3, la température commence à diminuer progressivement, et à l'instant t4 elle redevient égale à la valeur initiale (T0).

Ainsi, il est possible d'écrire l'équation du bilan thermique, une équation différentielle pour le chauffage du conducteur, une équation différentielle où il sera reflété que la chaleur libérée sur le conducteur est partiellement absorbée par le conducteur lui-même, et en partie est donnée à l'environnement. Voici l'équation:

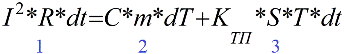
Sur le côté gauche de l'équation (1) se trouve la quantité de chaleur libérée dans le conducteur pendant le temps dt, le passage du courant I.

Le premier terme sur le côté droit de l'équation (2) est la quantité de chaleur absorbée par le matériau conducteur, à partir de laquelle la température du conducteur a augmenté de dT degrés.

Le deuxième terme sur le côté droit de l'équation (3) est la quantité de chaleur qui a été transférée du conducteur à l'environnement pendant le temps dt, et elle est liée à la surface du conducteur S et à la différence de température T à travers le coefficient de conductivité thermique Ktp.

Tout d'abord, lorsque le courant est activé, toute la chaleur dégagée dans le conducteur est utilisée pour chauffer directement le conducteur, ce qui entraîne une augmentation de sa température, et cela est dû à la capacité thermique C du matériau conducteur.

Avec l'augmentation de la température, la différence de température T entre le conducteur lui-même et l'environnement augmente en conséquence, et la chaleur générée va déjà partiellement augmenter la température ambiante.

Lorsque la température du conducteur atteint une valeur stable et constante de Tust, à ce moment-là, toute la chaleur dégagée par la surface du conducteur est transférée dans l'environnement, de sorte que la température du conducteur n'augmente plus.

La solution à l'équation du bilan thermique différentiel sera:

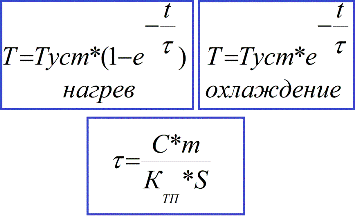
En pratique, ce processus transitoire ne dure pas plus de trois constantes de temps (3 * τ), et après ce temps, la température atteint 0,95 * Tust. Lorsque le processus de transition du chauffage s'arrête, l'équation du bilan thermique est simplifiée et la température en régime permanent peut facilement être exprimée:

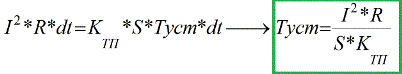
Courant admissible

Nous pouvons maintenant déterminer quelle valeur exacte le courant semble être un courant admissible à long terme pour un conducteur ou un câble. Évidemment, pour chaque conducteur ou câble, il existe une certaine température continue normale, selon sa documentation.C'est une telle température à laquelle un câble ou un fil peut être continuellement et pendant longtemps sans se nuire à lui-même et aux autres.

D'après l'équation ci-dessus, il devient clair qu'une valeur de courant spécifique est associée à une telle température. Ce courant est appelé courant de câble admissible. Il s'agit d'un tel courant qui, lorsqu'il traverse le conducteur pendant une longue période (plus de trois constantes de temps), le chauffe à une température admissible, c'est-à-dire Tdd normale.

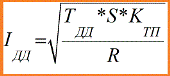
Ici: Idd - courant conducteur admissible à long terme; TDD - température admissible du conducteur.

Pour résoudre des problèmes pratiques, il est plus pratique de déterminer le courant admissible à long terme en fonction des tables spéciales du PUE.

Type de conducteur

Température admissible

Température admissible à court terme

Conducteur nu ou bus

70^{à propos}Avec

Cuivre - 300^{à propos}Avec

Conducteur nu ou bus

70^{à propos}Avec

Aluminium - 200^{à propos}Avec

Câble en isolation papier jusqu'à 3 kV

80^{à propos}Avec

200^{à propos}Avec

Câble en papier isolant jusqu'à 6 kV

65^{à propos}Avec

200^{à propos}Avec

Câble en papier isolant jusqu'à 10 kV

60^{à propos}Avec

200^{à propos}Avec

Câble en isolation papier jusqu'à 35 kV

50^{à propos}Avec

125^{à propos}Avec

Câble en isolation caoutchouc jusqu'à 1 kV

65^{à propos}Avec

150^{à propos}Avec

Câble en isolation PVC jusqu'à 1 kV

65^{à propos}Avec

150^{à propos}Avec

Câble isolé XLPE jusqu'à 1 kV

90^{à propos}Avec

250^{à propos}Avec

En cas de court-circuit, un courant de court-circuit important traverse le conducteur, ce qui peut chauffer considérablement le conducteur, dépassant sa température normale. Pour cette raison, les conducteurs sont caractérisés par une section minimale basée sur la condition de chauffage à court terme du conducteur par un courant de court-circuit:

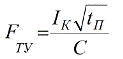
Ici: Ik - courant de court-circuit en ampères; tp est la durée réduite du courant de court-circuit en secondes; C est un coefficient qui dépend du matériau et de la construction du conducteur, et de la température admissible à court terme.

Connexion de section

Voyons maintenant comment le courant admissible à long terme dépend de la section du conducteur. Après avoir exprimé l'aire de la paroi latérale à travers le diamètre du conducteur (la formule au début de l'article), en supposant que la résistance est liée à l'aire de la section transversale et à la résistance spécifique du matériau du conducteur, et en remplaçant la formule bien connue de résistance dans la formule pour Idd, donnée ci-dessus, nous obtenons pour une formule Idd actuelle admissible à long terme :

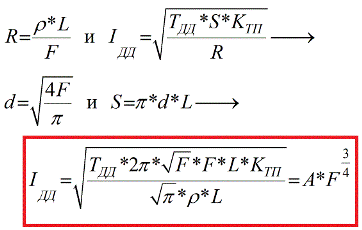
Il est facile de voir que la relation entre le courant admissible à long terme du conducteur Idd et la section F n'est pas directement proportionnelle, ici la section transversale est élevée à la puissance ¾, ce qui signifie que le courant admissible à long terme augmente plus lentement que la section transversale du conducteur. D'autres constantes, telles que la résistivité, le coefficient de transfert de chaleur, la température admissible, sont individuelles par définition pour chaque conducteur.

En fait, c'est que la dépendance ne peut pas être directe, car plus la section transversale du conducteur est grande, plus les conditions de refroidissement des couches internes du conducteur sont mauvaises, plus la température acceptable est atteinte à une densité de courant plus faible.

Si vous utilisez des conducteurs de plus grande section pour éviter une surchauffe, cela entraînera une consommation excessive de matériau. Il est beaucoup plus rentable d'utiliser plusieurs conducteurs de petite section disposés en parallèle, c'est-à-dire d'utiliser des conducteurs ou des câbles multiconducteurs. Et la relation entre le courant admissible à long terme et la section transversale dans son ensemble se présente comme suit:

F

1

2

4

Jedd

1

1,68

2,83

Courant et température

Pour calculer la température du conducteur à un courant connu et dans des conditions externes données, considérez l'état stationnaire lorsque la température du conducteur atteint Tust et ne croît plus. Données initiales - courant I, coefficient de transfert de chaleur Ktp, résistance R, surface de paroi latérale S, température ambiante T0:

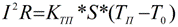
Un calcul similaire pour le courant continu:

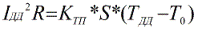
Ici, T0 est considéré comme la température ambiante calculée, par exemple + 15 ° C pour une pose sous l'eau et dans le sol, ou + 25 ° C pour une pose à l'air libre. Les résultats de ces calculs sont donnés dans tableaux des courants continus, et pour l'air ils prennent une température de + 25 ° C, car c'est la température moyenne du mois le plus chaud.

En divisant la première équation par la seconde et en exprimant la température du conducteur, nous pouvons obtenir une formule pour trouver la température du conducteur à un courant autre que le long terme admissible, et à une température ambiante donnée, si un courant admissible à long terme et une température admissible à long terme sont connus, et vous n'avez pas besoin de recourir à d'autres constantes:

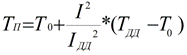
D'après cette formule, on peut voir que l'augmentation de la température est proportionnelle au carré du courant, et si le courant augmente de 2 fois, l'augmentation de la température augmentera de 4 fois.

Si les conditions extérieures diffèrent de la conception

En fonction des conditions extérieures réelles, qui peuvent différer de celles calculées en fonction du mode de pose, par exemple, plusieurs conducteurs parallèles en parallèle (câble) ou posés dans le sol à une température différente, un ajustement du courant maximal admissible est nécessaire.

Ensuite, le facteur de correction Kt est introduit, par lequel le courant admissible à long terme est multiplié dans des conditions connues (tabulaires). Si la température extérieure est inférieure à celle calculée, alors le coefficient est supérieur à un; s'il est supérieur à celui calculé, alors, en conséquence, Kt est inférieur à un.

Lors de la pose de plusieurs conducteurs parallèles très proches les uns des autres, ils se chauffent également les uns les autres, mais uniquement si l'environnement est stationnaire. Les conditions réelles conduisent souvent au fait que l'environnement est mobile (air, eau), et la convection conduit au refroidissement des conducteurs.

Si le milieu est presque stationnaire, par exemple, lors de la pose dans une conduite souterraine ou dans un conduit, un échauffement mutuel entraînera une diminution du courant admissible à long terme, et ici vous devez saisir à nouveau le facteur de correction Kn, qui est indiqué dans la documentation pour les câbles et les fils.

Comments

[#1]

En général, chaque fournisseur de fils ou de câbles qui se respecte fournit aujourd'hui des tableaux d'accompagnement, où pour un fil particulier dans diverses conditions, vous pouvez facilement trouver un courant admissible à long terme et ne pas vous tromper. Le fabricant effectue lui-même tous les calculs et calculs nécessaires, et le consommateur ne peut choisir dans le tableau qu'un câble ou un fil de section appropriée et la modification requise.

[#2 Anatoly]

C'est vrai! Mais non seulement lors de la pose du câble dans le sol, mais aussi lors de la pose directement dans les grilles sous le plâtre, les conditions de pose du câble peuvent différer de celles calculées (malheureusement, dans les documents réglementaires et techniques, y compris le PUE, ce problème n'est pas pris en compte), d'où les erreurs lors de la pose du câble. Par exemple, selon le PUE, le courant nominal du câble lors de sa pose dans le tuyau, et l'ondulation PVC est essentiellement un tuyau PVC souple, le courant nominal du câble, avec un facteur de remplissage de l'ondulation avec un câble de 0,3 - 0,5, est de 21 ampères, et dans le sable - plâtre de ciment - 20 ampères. Si vous utilisez GOST RM EK 60287 - 2 - 1 - 2009, sachant que la résistance thermique du plâtre sable-ciment est en moyenne de 1 (m * degrés Celsius / Watt) et la résistance thermique du poumon de béton cellulaire est égal à 10 (m * degré Celsius / Watt), nous obtenons que le courant nominal du courant de câble dans le béton cellulaire est de 20 * 20/10 = 40, nous extrayons la racine carrée et obtenons environ 7,1 ampères, la pratique d'exploitation a montré qu'en conditions de pose réelles, lorsque un côté est recouvert de gypse, le courant nominal du câble est d'environ 10 ampères, deux fois et moins que dans le plâtre de sable et de ciment. La même chose s'applique à d'autres matériaux de construction. Si le câble s'étend sur une section étendue de béton cellulaire, de gypse, etc., selon le PUE, le courant nominal du câble doit être sélectionné en fonction des pires conditions de pose ou de courant à 10 ampères et un disjoncteur cayuel de 6 ampères. MAIS, si vous posez le câble, ainsi que le fil, pour que la gaine ne l'empêche pas de mieux refroidir, alors le courant nominal du câble est de 21 ampères, car l'environnement de sa pose n'a pas changé.Et la pratique d'exploitation le confirme. Ainsi, le but le plus important d'une ondulation est de préserver le courant nominal du câble quelles que soient les conditions de sa pose, c'est-à-dire quelle que soit la résistance thermique des matériaux sur lesquels le câble est posé. L'ondulation est spécialement conçue pour répondre à cette exigence préservant le courant nominal du câble, l'énergie thermique dégagée par le câble est absorbée par l'air dans l'ondulation et le matériau de l'ondulation lui-même par convection et rayonnement thermique, et le transfert de chaleur ne joue pas un rôle important le rôle du refroidissement du câble, en raison de la très grande résistance thermique de l'air et de l'ondulation elle-même, bien sûr, lors de la pose sur des matériaux à faible résistance thermique, la température de l'ondulation diminue et il est capable d'absorber plus d'énergie thermique, mais cette réduction n'est pas significative. Même lors de la pose du câble dans l'ondulation en béton cellulaire , la résistance thermique du béton cellulaire ne dépasse pas 18 à 20% de la résistance thermique de l'air dans l'ondulation. Autrement dit, même avec une résistance infiniment grande de l'environnement extérieur de pose de l'ondulation, le câble au courant nominal n'est pas chauffé La température sera supérieure à la température autorisée et, dans un environnement à faible résistance thermique, le câble aura une température lors de sa pose dans l'ondulation encore plus basse que la température maximale autorisée. L'ondulation a été créée à la place des tuyaux en acier, lorsque divers matériaux ayant une résistance thermique différente le long des voies de pose des câbles ont commencé à être utilisés dans la construction .

[#3 Nikolay]

Tout courant circulant en continu dans des conditions externes constantes correspond à une température à l'état stable bien définie du conducteur. L'amplitude du courant de longue durée auquel la température devient le maximum admissible pour une marque donnée de fil ou de câble est appelée la charge de courant à long terme.

L'amplitude du courant admissible à long terme dépend du matériau et de la section du conducteur, de la température ambiante, du matériau d'isolation et de la méthode de pose. Le mode de fonctionnement des fils et câbles est également important. En fonctionnement intermittent, la charge de courant admissible peut être augmentée. Pour déterminer la valeur du courant admissible à long terme, il est important de connaître la température ambiante positive la plus élevée, car à basses températures au même courant, des conditions de travail plus favorables des fils et des câbles sont fournies.

[#4 Alex]

Ce n'est pas clair - comme pour un fil de section carrée de 2 mm, l'intensité du courant n'est que de 1,68 A ???

25A vous pouvez à la légère, je ne comprends rien ...